|
||||||||||
| Modellazione e rendering di un anello (prima parte) Questo tutorial si propone di analizzare alcuni aspetti della modellazione NURBS in Rhino applicati al design di un anello, tra cui: il grado di una curva, la continuità di curvatura tra le curve, l'azione del comando Match curve, l'azione del comando Split, l'uso dei layer, gli effetti e i difetti delle operazioni booleane. Per seguire questo tutorial è richiesta solo una conoscenza minima del programma. In particolare della tecnica base di selezione degli oggetti che, si ricorda, è da confermare con la pressione di [Invio] sulla tastiera, come da richiesta nella riga di comando. |
||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
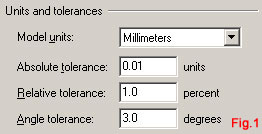
| Avviamo il programma e verifichiamo che la voce Units, della finestra Rhino Options, sia impostata come in fig.1. Lavoreremo con i millimetri. Attiviamo la voce Snap nella barra di stato (fig.2). Di default lo snap è impostato su una unità, quindi nel nostro caso su 1mm. Impostiamo anche la barra degli strumenti relativa agli osnap persistenti, come in fig.2. | ||||||||||||||||||||||||||||||
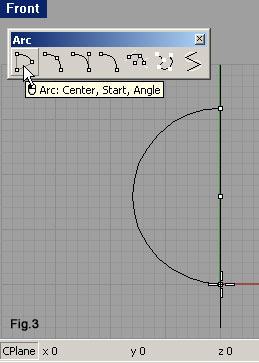
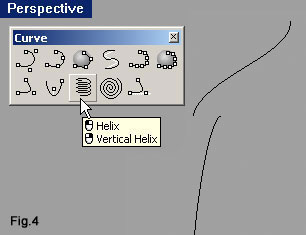
| Avviamo il comando per il disegno degli archi con l'icona indicata in fig.3. Sfruttando lo snap indichiamo, nella finestra Front (fig.3), il punto 0,8 poi 0,16 infine 0,0 (sulla barra di stato si verifica facilmente la posizione del cursore). Con l'icona Helix della barra degli strumenti Curve (fig.4), avviamo il comando per il disegno delle eliche. Per il punto iniziale dell’asse, digitiamo 0,-1,16 quindi per il punto finale r0,0,5 verifichiamo che l'opzione Mode sia impostata su Turns, che Turns sia pari a 0.5 e che sia attivo ReverseTwist; quindi quale punto iniziale dell'elica immettiamo 0,1.5,16. Le linee di comando che si svolgono sono simile a queste: Command: _Helix Start of axis ( Vertical AroundCurve ): 0,-1,16 End of axis: r0,0,5 Radius and start point <1.000> ( Diameter Mode=Turns Turns=0.5 Pitch=8 ReverseTwist=Yes ): 0,1.5,16 Ne ricaveremo un'elica che si sviluppa per metà spira, con raggio pari a 2.5mm, lungo un asse di 5mm. |
||||||||||||||||||||||||||||||
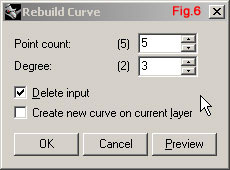
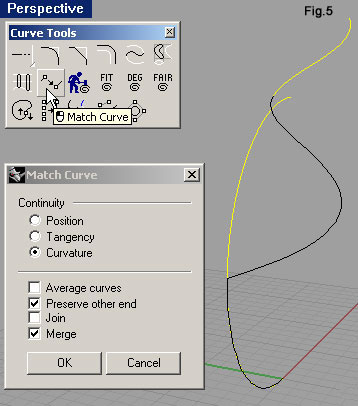
| Ci proponiamo ora di fondere, con continuità di curvatura, queste due curve per ricavarne un'unica; la cui forma derivi dalle condizioni di continuità. Se agissimo direttamente sull'arco così come disegnato, ne constateremmo uno strano comportamento: la curva si piegherebbe bruscamente a metà della sua lunghezza (fig.5). Questa inaspettata piegatura si spiega con l’insufficiente grado della curva: un arco, in quanto curva piana, è generata con grado due (ancora una volta è necessario conoscere veramente le NURBS). Per procedere correttamente è allora indispensabile aumentare il grado della curva. È sufficiente richiamare l’icona Rebuild della barra degli strumenti Curve Tools, selezionare l’arco e impostare la relativa finestra come in fig.6 per portare il grado della curva a 3 (quello minimo per garantire sufficiente flessibilità a una curva sghemba). | ||||||||||||||||||||||||||||||
 |
 |
|||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
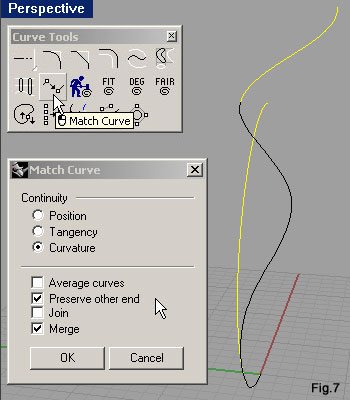
| Possiamo procedere con la fusione delle curve, agendo nella finestra Perspective. Facciamo click sull’icona Match curve della barra degli strumenti Curve Tools, selezioniamo quindi prima l’arco (la curva che si deve piegare) poi l’elica. Impostiamo la finestra di dialogo che si apre come in fig.7. La casella di controllo Merge, farà in modo che le due curve, oltre che venire a contatto, si fondano in un’unica. La curva così prodotta non può più essere esplosa, diversamente da quanto produce la casella di controllo Join. | ||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
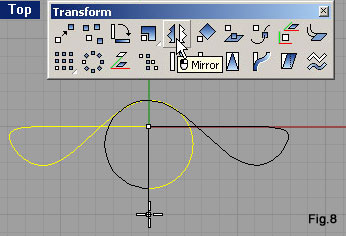
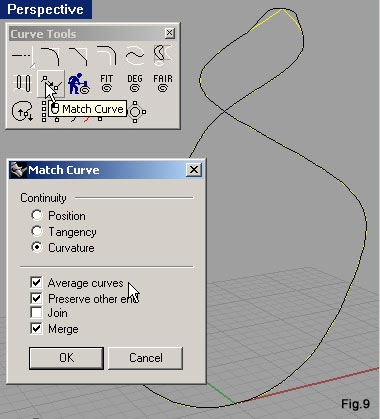
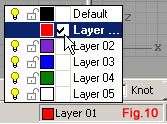
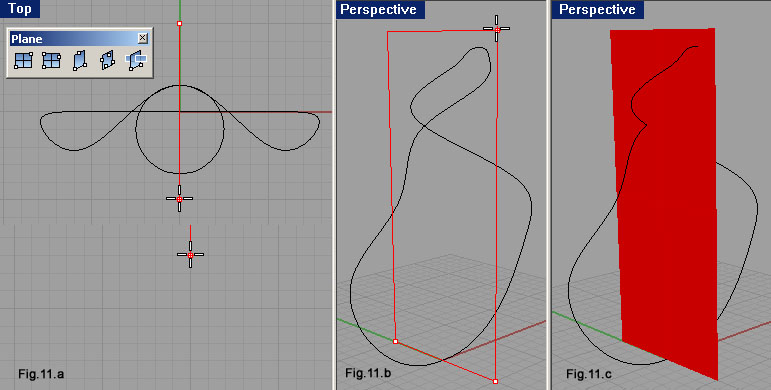
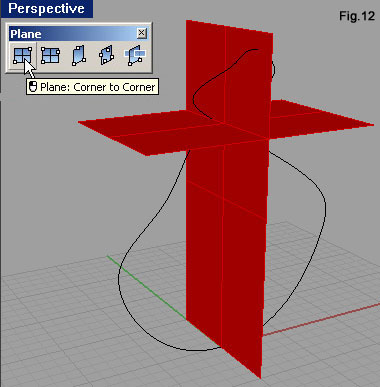
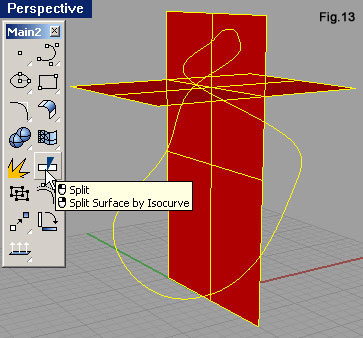
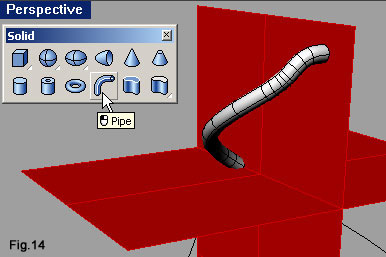
| Agendo nella finestra Top, con il comando Mirror (fig.8), specchiamo la curva rispetto all’asse Y del CPA (quello verde). Lanciato il comando si deve selezionare l’oggetto, confermare la sua selezione con [Invio], quindi indicare due punti ad ascissa nulla sfruttando il semplice snap. Anche queste due curve vanno fuse, per eliminare il loro punto di contatto più in alto angoloso. Riutilizziamo Match curve, questa volta però attivando la casella di controllo Average curve (fig.9), così da modificare entrambe le curve (la deformazione di distribuisce al 50% su ciascuna). La curva ora ricavata costituisce il percorso che deve seguire la sezione della “struttura” dell’anello. Questo percorso ha però una terribile particolarità: si autointerseca. Lo sviluppo che ne deriverebbe è di conseguenza autocompenetrante. Una situazione del genere può creare problemi a software che producono modellazione solida, visto come distinguono l’interno dall’esterno del modello. Una soluzione potrebbe prevedere comunque lo sviluppo di questo profilo a cui far seguire delle operazioni necessarie a dividere in quattro parti la polisuperficie che se ne ricava. A questa soluzione preferiremo quella che prevede la divisione della curva in quattro parti, così da procedere con estrusioni distinte. Con un click nell’area dei layer nella barra di stato (fig.10), apriamo il relativo menù in cui fare click sul riquadro di Layer 01, per renderlo corrente. Disegneremo su di esso due superfici piane da sfruttare per dividere in quattro parti la curva. Richiamiamo l’icona Vertical Plane della barra degli strumenti Plane. Indichiamo due punti lungo l’asse Y del CPA della finestra Top, come in fig.11.a. Portiamo quindi il cursore nella finestra Perspective e qui indichiamo un terzo punto che abbia quota maggiore del punto più alto della curva (fig.11.b). Ne ricaveremo un piano che tagli completamente la curva (fig.11.c). Attiviamo ora la viewport Top e facciamo click sull’icona Plane: Corner to Corner, digitiamo le coordinate come riportato in queste righe di comando: Command: _Plane First corner of plane (3Point Vertical Center Deformable): -8,-5,16 Other corner or length: 8,5,16 Un'altra superficie piana (fig.12), taglia orizzontalmente la curva lì dove dovrà essere divisa. Lanciamo Split, selezioniamo la curva a confermiamo con [Invio] sulla tastiera, selezioniamo i due piani (fig.13) e confermiamo ancora con [Invio]. Possiamo rendere corrente il layer Default. Avviamo il comando per produrre “tubi” tramite l’icona Pipe della barra degli strumenti Solid. Selezioniamo la curva superiore sinistra (fig.14) e indichiamo come raggio iniziale del tubo 0.3. Come raggio finale del tubo indichiamo ancora 0.3. |
||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
 |
 |
|||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
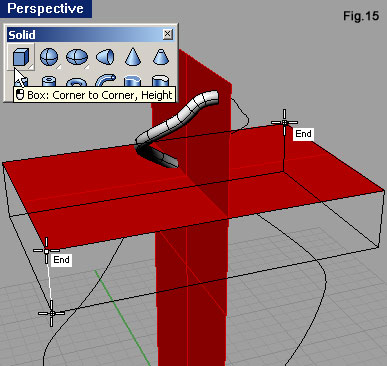
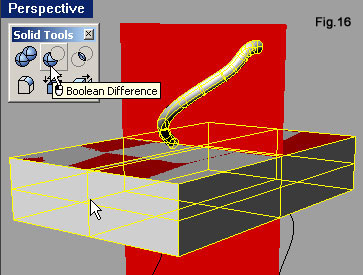
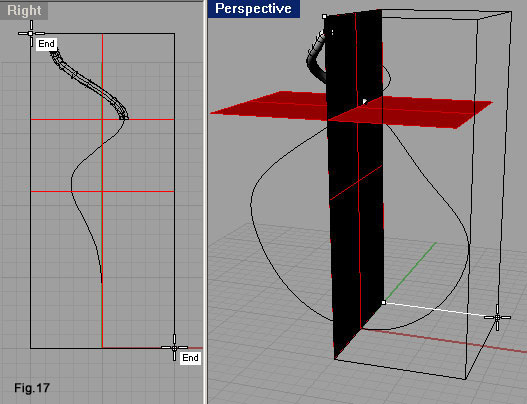
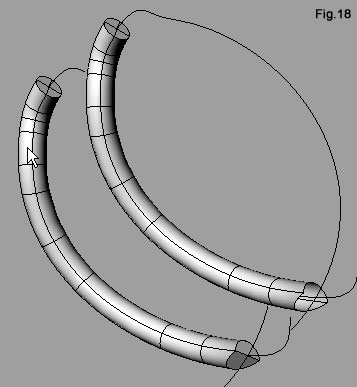
| Avviamo il comando Box (fig.15) e, agendo nella finestra Perspective, grazie all’osnap End, agganciamo due vertici diametralmente opposti della superficie piana orizzontale, quindi indichiamo un terzo punto con quota inferiore (fig.15). Avviamo ora la sottrazione booleana con l’icona Boolean Difference della barra degli strumenti Solid Tools (fig.16), selezioniamo il tubo e confermiamo con [Invio], quindi selezioniamo il parallelepipedo e confermiamo ancora con [Invio]. Il parallelepipedo toglierà la porzione di tubo che andrebbe a sovrapporsi con quello ricavato con la linea inferiore sinistra. Operazione simile si deve eseguire per eliminare quella porzione di tubo che andrebbe a sovrapporsi con quello ricavato dalla curva superiore destra. Il parallelepipedo sottraente si disegna più facilmente sfruttando l’osnap End per indicare nella finestra Right (fig.17) i primi due punti, per poi passare alla finestra Perspective dove indicare il terzo che fornisce spessore al solido. Lo stesso risultato non si poteva raggiungere operando dei tagli con il comando Trim, sfruttando le superfici piane come limite di taglio: si sarebbe ricavata una polisuperficie non più un solido. Osservando la fig.18 si può notare il diverso effetto delle operazioni booleane rispetto al taglio. Nel secondo caso, il solido avrebbe perso delle facce. |
||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
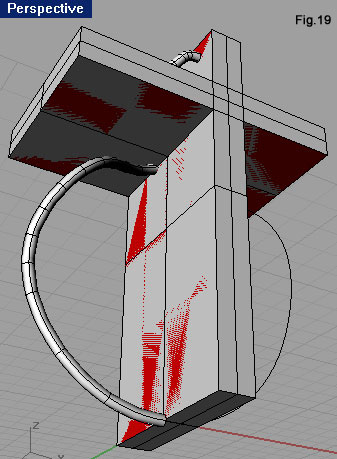
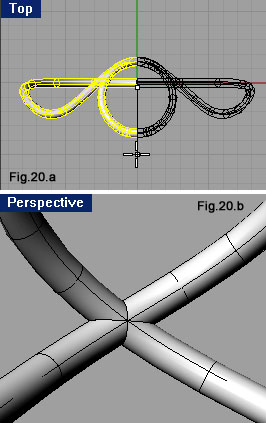
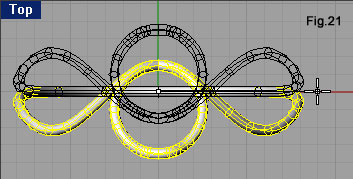
| Come fatto per la curva superiore sinistra, usiamo il comando Pipe su quella inferiore sinistra. Anche sul tubo ora ricavato dovremo agire con due sottrazioni booleane, utilizzando come solidi sottraenti un parallelepipedo posato sopra alla superficie piana orizzontale e uno adagiato sulla destra della superficie piana verticale (fig.19). Possiamo spegnere il Layer 01. Agendo nella finestra Top, con il comando Mirror, specchiamo i due tubi rispetto all’asse Y del CPA (fig.20.a). Grazie alle sottrazioni booleane praticate, non si verificano compenetrazioni (fig.20.b). Un modello prodotto secondo questo rigore, è quantomeno formalmente più corretto. Avviamo il comando Mirror, selezioniamo i quattro solidi e indichiamo come primo punto dell’asse di simmetria 0,0 come secondo r1,0 (fig.21). |
||||||||||||||||||||||||||||||
 |
 |
|||||||||||||||||||||||||||||
 |
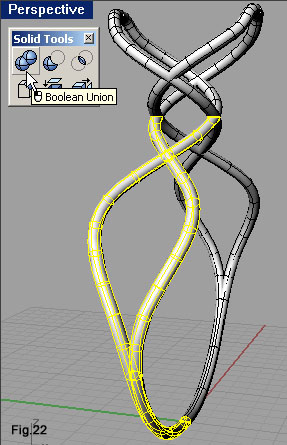
Non resterebbe che operare quattro unioni booleane tra le coppie di tubi che si compenetrano (fig.22), se non fosse che Rhino ha notevoli difficoltà su determinate operazioni booleane. Nel nostro caso, le due coppie di tubi superiori si uniscono, quelle inferiori no (nonostante non vi siano situazioni di autocompenetrazione)! Nella seconda parte del tutorial affronteremo la modellazione della pietra, nella terza il rendering dell'anello completo. |
|||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
